Today, we're diving into a topic that's a bit more technical but essential. I've briefly mentioned before how option contract prices are calculated. If you remember, the Nobel Prize-winning Black Scholes Merton differential equation determined the value of contracts. Let's first take a look at this equation.
Economists Fischer Black and Myron Scholes invented the risk-neutral argument in 1968 by showing that a dynamic revision of a portfolio eliminated the expected return of the security. They first applied this formula to the market but went bankrupt due to a lack of risk management. In 1970, they returned to academic work and started working on the formula. After 3 years of work, they published a paper titled "The Pricing of Options and Corporate Liabilities." A mathematical model is an attempt to translate the behavior of some system into mathematical language. By doing so it can allow for better understanding of the system more powerful analysis as well as testing the effect of changes. It is also what is used to calculate the greeks.
The fundamental principle behind the model is to hedge the option by buying and selling the underlying asset in a specific way to eliminate risk. This type of hedging is called "continuously revised delta hedging" and forms the basis of more complex hedging strategies used by investment banks and hedge funds.

The formula led to a boom in options trading and provided mathematical legitimacy to the activities of the Chicago Board Options Exchange and other options markets around the world. Robert C. Merton was the first to publish a paper expanding the mathematical understanding of the options pricing model and coined the term "Black-Scholes options pricing model." Merton contributed to Black and Scholes' paper. In 1997, Scholes and Merton jointly won the Nobel Prize in Economics for their work. Fisher Black couldn't receive the award as he passed away in 1995.
Understanding why this is so important and why it won a Nobel Prize isn't actually difficult, although it might seem simple to us. Valuing a product 1 month or 3 months into the future is really challenging, especially with somewhat high inflation, interest rates, and in the product being valued. And a fair agreement is needed where neither the buyer nor the seller wants to transfer their risk to the other party. They create such an equation for the calculation to be real and appealing to everyone.

Let's look at the important indicators here. At the same time, let's examine how compatible the formula is with the real-life market and what the changes could be.
N(x) = The normal distribution of daily returns of a good is examined. How the daily return of a product is distributed is one of the most important factors in valuing a product.
T = Time left until expiration
S = Current price of the product
K = The price at which the agreement will be made
r = Interest rate of the currency in which the product is traded (The risk-free return of the product is as much as the interest rate of the opposing asset)
σ = Annual volatility of the product
Increasing the underlying price will increase the price of calls, and decrease the price of puts.
Increasing the strike price will decrease the price of calls, and increase the price of puts.
As time passes (decreasing DTE) both calls and puts will lose value.
Increasing the interest rate will increase the price of calls, and decrease the price of puts.
Increasing implied volatility will increase the price of both calls and puts.
You can see the Basic Hypotheses of the Black-Scholes Model in the image below. The most striking thing here is "Random Walk." It's the assumption that the price moves completely randomly, just as we can't know where a piece of branch floating on water will be in 1 minute (see: Brownian Motion), we can't know where the price will be in 1 day, month, or year.
If you don't accept this, you can stop reading the article here, because you're saying you can know the price and you can bet all your money on that condition.

Let's solve an example and see how the formula works in real market conditions.
You can make your own calculation from sites. I found the annual volatility by converting the average of the daily volatility in the month.
You can see the data I took from my notes here.

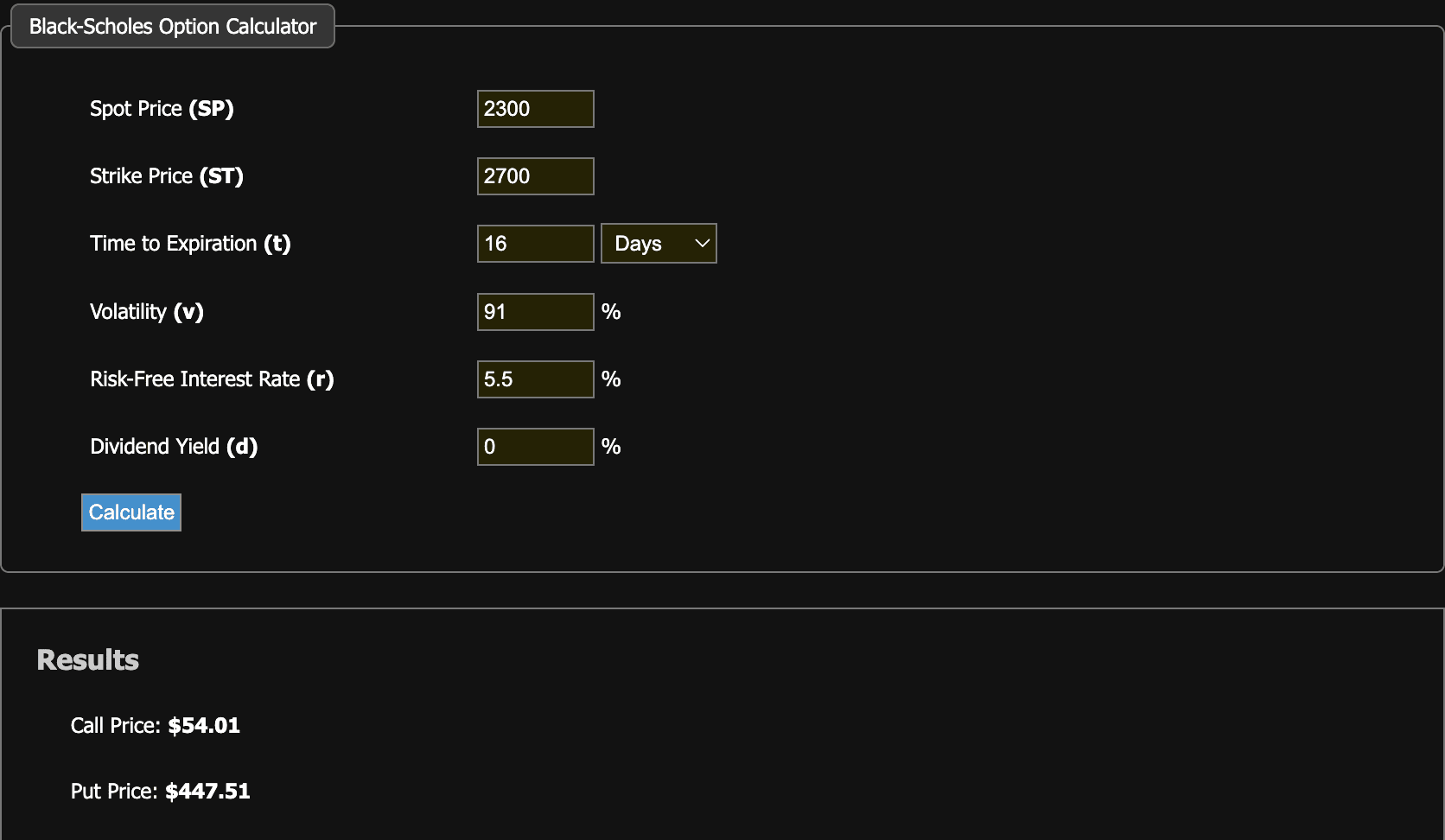
As you can see, the calculation found the Call price for the September 27, 2024 ETH 2700 Contract to be $54, and the Put contract price to be $447. Well, what are the current prices in real market conditions?
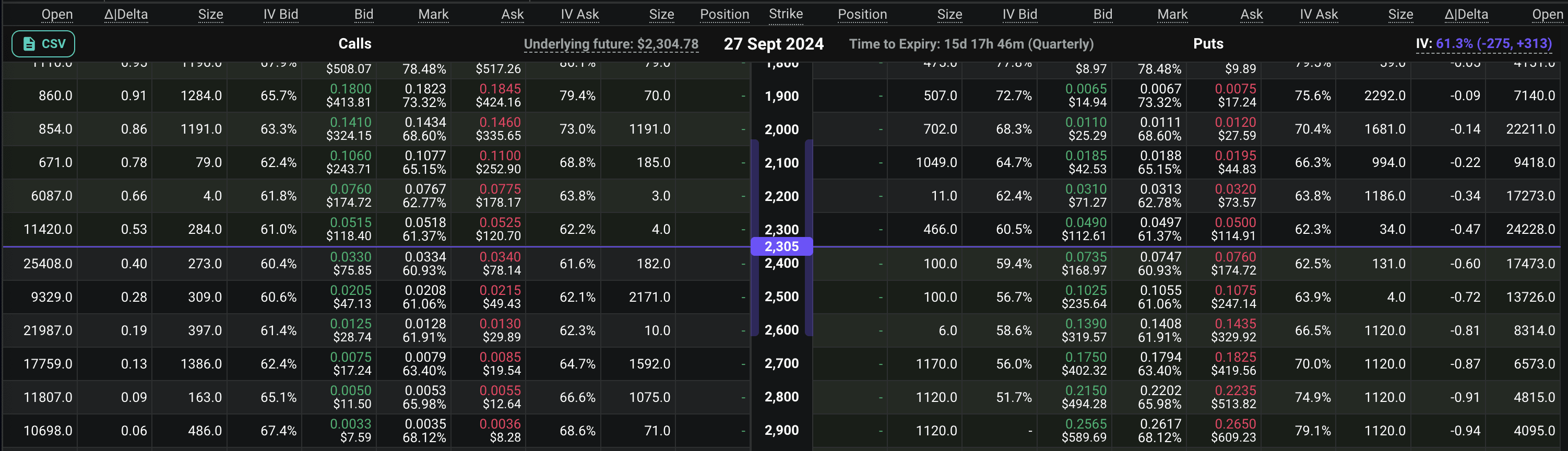
Yes, you're not seeing it wrong, the Call price is around $18, and the Put price is around $410. So why is there such a big difference? Please think about it first, before reading what I've written below, take a look at the table and try to find out what could be such a big factor, why those selling Call contracts want to sell their contracts at such a low price.
If you're ready, go back to the table and look at the percentages in the "IV Ask" section, and you'll see your answer. IV, as you remember, is the abbreviation for Implied Volatility. In other words, those selling this contract don't expect 90% annual volatility, they expect about 65% volatility. The fact that the price is much below the mathematical average also shows how much the demand has decreased and that Implied Volatility has decreased for this reason. In the context of this contract, our market's volatility expectation is around 65%. Well, let's try and verify it.
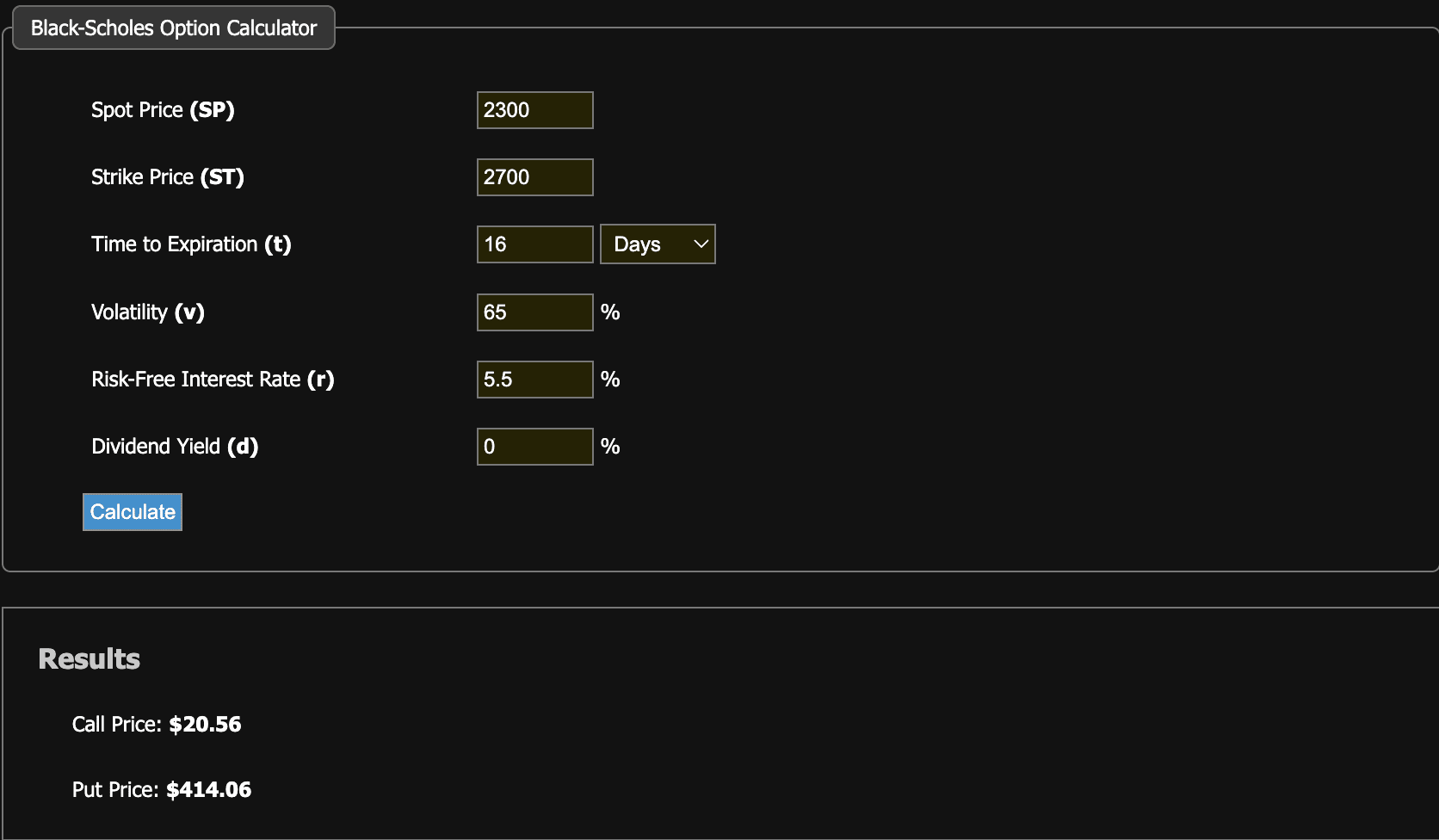
As you can see, it has come to the current market price. This is the biggest indicator of real market conditions and that the price moves randomly. You can use this data not only for options but also to see how likely the price you expect is in your own charts. The VIX Index, which is very popular now, is calculated from a large number of contracts of about 100 products. It's also known as the fear index.
As you can see from here, we actually look at the charts we should look at last, first. In our analyses, you need to see the expectations of the big market makers, see the implied volatility, and then make an analysis by considering the importance of those levels by looking at the charts. Because the data visible from the beginning of the article are not an analysis but data directly showing the real market. It absolutely reflects the market. But let's not forget that these data include expectations from now until September 27. When factors such as news, volatility changes occur tomorrow, these data will also be affected.
I'll give one last bit of information and end my article while you think about this until the next article. We found the price of the contract, we valued a product, but how does the price of this contract continue to be valued so quickly in market conditions? Does the contract price increase to the same degree as the spot price increases? In other words, when ETH goes from 2300 to 2320, does the contract price increase by $20 or less? What happens if volatility increases or interest rates change? We use Greeks for such questions. For now, I'm ending with a brief definition. Wishing you days with better analysis.
Options Greeks

#CPI_BTC_Watch #BinanceBlockchainWeek #BlackScholes #OptionsTrading #OptionsExpiration $ETH $BTC
