Satoshi Nakamoto
satoshin@gmx.com
www.bitcoin.org

Résumé : Une version purement peer-to-peer de la monnaie électronique permettrait d'envoyer des paiements en ligne directement d'une partie à une autre sans passer par une institution financière. Les signatures numériques constituent une partie de la solution, mais les principaux avantages sont perdus si un tiers de confiance est toujours requis pour éviter les doubles dépenses. Nous proposons une solution au problème de la double dépense en utilisant un réseau peer-to-peer. Le réseau horodate les transactions en les hachant dans une chaîne continue de preuves de travail basées sur le hachage, formant ainsi un enregistrement qui ne peut pas être modifié sans refaire la preuve de travail. La chaîne la plus longue sert non seulement de preuve de la séquence d’événements observée, mais aussi de preuve qu’elle provient du plus grand pool de puissance CPU. Tant que la majorité de la puissance du processeur est contrôlée par des nœuds qui ne coopèrent pas pour attaquer le réseau, ils généreront la chaîne la plus longue et devanceront les attaquants. Le réseau lui-même nécessite une structure minimale. Les messages sont diffusés au mieux et les nœuds peuvent quitter et rejoindre le réseau à volonté, acceptant la plus longue chaîne de preuve de travail comme preuve de ce qui s'est passé pendant leur absence.
1. Introduction
Le commerce sur Internet dépend désormais presque exclusivement des institutions financières faisant office de tiers de confiance pour traiter les paiements électroniques. Bien que le système fonctionne assez bien pour la plupart des transactions, il souffre toujours des faiblesses inhérentes au modèle basé sur la confiance. Des transactions totalement irréversibles ne sont pas vraiment possibles, dans la mesure où les institutions financières ne peuvent éviter de jouer un rôle de médiateur dans les différends. Le coût de la médiation augmente les coûts de transaction, limitant la taille minimale pratique des transactions et supprimant la possibilité de petites transactions occasionnelles, et il existe un coût plus important lié à la perte de capacité à effectuer des paiements irréversibles pour des services irréversibles. Avec la possibilité d’un renversement, le besoin de confiance se propage. Les commerçants doivent se méfier de leurs clients, en les harcelant pour obtenir plus d’informations qu’ils n’en auraient autrement besoin. Un certain pourcentage de fraude est considéré comme inévitable. Ces coûts et incertitudes de paiement peuvent être évités en personne en utilisant de la monnaie physique, mais aucun mécanisme n'existe pour effectuer des paiements via un canal de communication sans une partie de confiance.
Ce qu’il faut, c’est un système de paiement électronique basé sur une preuve cryptographique plutôt que sur la confiance, permettant à deux parties volontaires d’effectuer des transactions directement entre elles sans avoir besoin d’un tiers de confiance. Les transactions qu'il est impossible d'annuler sur le plan informatique protégeraient les vendeurs contre la fraude, et des mécanismes de dépôt de routine pourraient facilement être mis en œuvre pour protéger les acheteurs. Dans cet article, nous proposons une solution au problème de la double dépense en utilisant un serveur d'horodatage distribué peer-to-peer pour générer une preuve informatique de l'ordre chronologique des transactions. Le système est sécurisé tant que les nœuds honnêtes contrôlent collectivement plus de puissance CPU que n’importe quel groupe de nœuds attaquants coopérants.
2. Opérations
Nous définissons une pièce électronique comme une chaîne de signatures numériques. Chaque propriétaire transfère la pièce au suivant en signant numériquement un hachage de la transaction précédente et la clé publique du prochain propriétaire et en les ajoutant à la fin de la pièce. Un bénéficiaire peut vérifier les signatures pour vérifier la chaîne de propriété.

Le problème est bien sûr que le bénéficiaire ne peut pas vérifier que l’un des propriétaires n’a pas dépensé deux fois la pièce. Une solution courante consiste à introduire une autorité centrale de confiance, ou menthe, qui vérifie chaque transaction pour déceler une double dépense. Après chaque transaction, la pièce doit être retournée à la Monnaie pour émettre une nouvelle pièce, et seules les pièces émises directement par la Monnaie sont censées ne pas être dépensées en double. Le problème avec cette solution est que le sort de l’ensemble du système monétaire dépend de l’entreprise qui gère la monnaie, chaque transaction devant passer par elle, tout comme une banque. Nous avons besoin d'un moyen pour que le bénéficiaire sache que les propriétaires précédents n'ont signé aucune transaction antérieure. Pour nos besoins, la première transaction est celle qui compte, nous ne nous soucions donc pas des tentatives ultérieures de double dépense. La seule façon de confirmer l’absence de transaction est d’être au courant de toutes les transactions. Dans le modèle basé sur la monnaie, la monnaie était au courant de toutes les transactions et décidait laquelle arrivait en premier. Pour y parvenir sans partie de confiance, les transactions doivent être annoncées publiquement [1], et nous avons besoin d'un système permettant aux participants de se mettre d'accord sur un historique unique de l'ordre dans lequel elles ont été reçues. Le bénéficiaire a besoin de la preuve qu'au moment de chaque transaction, la majorité des nœuds ont convenu qu'il s'agissait du premier reçu.
3. Serveur d'horodatage
La solution que nous proposons commence par un serveur d'horodatage. Un serveur d'horodatage fonctionne en prenant un hachage d'un bloc d'éléments à horodater et en publiant largement le hachage, comme dans un journal ou une publication Usenet [2-5]. L'horodatage prouve que les données doivent évidemment avoir existé à ce moment-là pour entrer dans le hachage. Chaque horodatage inclut l'horodatage précédent dans son hachage, formant une chaîne, chaque horodatage supplémentaire renforçant ceux qui le précèdent.

4. Preuve de travail
Pour implémenter un serveur d'horodatage distribué sur une base peer-to-peer, nous devrons utiliser un système de preuve de travail similaire à Hashcash d'Adam Back [6], plutôt que des publications dans les journaux ou Usenet. La preuve de travail implique la recherche d'une valeur qui, une fois hachée, comme avec SHA-256, le hachage commence par un nombre de bits nuls. Le travail moyen requis est exponentiel en nombre de bits zéro requis et peut être vérifié en exécutant un seul hachage.
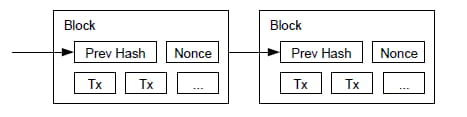
Pour notre réseau d'horodatage, nous implémentons la preuve de travail en incrémentant un nom occasionnel dans le bloc jusqu'à ce qu'une valeur soit trouvée qui donne au hachage du bloc les bits zéro requis. Une fois que l'effort CPU a été dépensé pour satisfaire la preuve de travail, le bloc ne peut plus être modifié sans refaire le travail. Comme les blocs ultérieurs sont enchaînés après celui-ci, le travail de modification du bloc impliquerait de refaire tous les blocs qui le suivent.
La preuve de travail résout également le problème de la détermination de la représentation dans la prise de décision majoritaire. Si la majorité était basée sur une adresse IP, un vote, elle pourrait être renversée par quiconque capable d'attribuer de nombreuses adresses IP. La preuve de travail repose essentiellement sur un processeur, un vote. La décision majoritaire est représentée par la chaîne la plus longue, dans laquelle est investi le plus grand effort de preuve de travail. Si la majorité de la puissance du processeur est contrôlée par des nœuds honnêtes, la chaîne honnête croîtra le plus rapidement et dépassera toutes les chaînes concurrentes. Pour modifier un bloc passé, un attaquant devrait refaire la preuve de travail du bloc et de tous les blocs suivants, puis rattraper et surpasser le travail des nœuds honnêtes. Nous montrerons plus tard que la probabilité qu’un attaquant plus lent rattrape son retard diminue de façon exponentielle à mesure que des blocs ultérieurs sont ajoutés.
Pour compenser l'augmentation de la vitesse du matériel et l'intérêt variable pour l'exécution des nœuds au fil du temps, la difficulté de la preuve de travail est déterminée par une moyenne mobile ciblant un nombre moyen de blocs par heure. S'ils sont générés trop rapidement, la difficulté augmente.
5. Réseau
Les étapes pour gérer le réseau sont les suivantes :
1) Les nouvelles transactions sont diffusées à tous les nœuds.
2) Chaque nœud collecte de nouvelles transactions dans un bloc.
3) Chaque nœud s'efforce de trouver une preuve de travail difficile pour son bloc.
4) Lorsqu'un nœud trouve une preuve de travail, il diffuse le bloc à tous les nœuds.
5) Les nœuds n'acceptent le bloc que si toutes les transactions qu'il contient sont valides et n'ont pas déjà été dépensées.
6) Les nœuds expriment leur acceptation du bloc en travaillant à la création du bloc suivant dans la chaîne, en utilisant le hachage du bloc accepté comme hachage précédent.
Les nœuds considèrent toujours que la chaîne la plus longue est la bonne et continueront à travailler pour l'étendre. Si deux nœuds diffusent simultanément des versions différentes du bloc suivant, certains nœuds peuvent recevoir l'une ou l'autre en premier. Dans ce cas, ils travaillent sur la première branche qu’ils ont reçue, mais gardent l’autre branche au cas où elle deviendrait plus longue. L'égalité sera rompue lorsque la prochaine preuve de travail sera trouvée et qu'une branche deviendra plus longue ; les nœuds qui travaillaient sur l'autre branche passeront alors à la plus longue.
Les nouvelles diffusions de transactions ne doivent pas nécessairement atteindre tous les nœuds. Tant qu’ils atteignent de nombreux nœuds, ils entreront bientôt dans un bloc. Les diffusions en bloc tolèrent également les messages supprimés. Si un nœud ne reçoit pas de bloc, il le demandera lorsqu'il recevra le bloc suivant et se rendra compte qu'il en a manqué un.
6. Incitation
Par convention, la première transaction dans un bloc est une transaction spéciale qui démarre une nouvelle pièce appartenant au créateur du bloc. Cela incite davantage les nœuds à prendre en charge le réseau et fournit un moyen de distribuer initialement les pièces en circulation puisqu'il n'y a pas d'autorité centrale pour les émettre. L’ajout constant d’une quantité constante de nouvelles pièces est analogue au fait que les mineurs d’or dépensent des ressources pour ajouter de l’or à la circulation. Dans notre cas, c'est du temps CPU et de l'électricité qui sont dépensés.
L'incitation peut également être financée par des frais de transaction. Si la valeur de sortie d'une transaction est inférieure à sa valeur d'entrée, la différence constitue des frais de transaction qui s'ajoutent à la valeur incitative du bloc contenant la transaction. Une fois qu’un nombre prédéterminé de pièces est entré en circulation, l’incitation peut passer entièrement aux frais de transaction et être totalement sans inflation.
L'incitation peut aider à encourager les nœuds à rester honnêtes. Si un attaquant cupide est capable d'assembler plus de puissance CPU que tous les nœuds honnêtes, il devra choisir entre l'utiliser pour frauder les gens en lui volant ses paiements ou l'utiliser pour générer de nouvelles pièces. Il devrait trouver plus rentable de respecter les règles, des règles qui le favorisent avec plus de nouvelles pièces que tous les autres réunis, plutôt que de saper le système et la validité de sa propre richesse.
7. Récupération d'espace disque
Une fois que la dernière transaction dans une pièce est enfouie sous suffisamment de blocs, les transactions dépensées avant elle peuvent être supprimées pour économiser de l'espace disque. Pour faciliter cela sans casser le hachage du bloc, les transactions sont hachées dans un arbre Merkle [7] [2] [5], avec seule la racine incluse dans le hachage du bloc. Les vieux blocs peuvent ensuite être compactés en coupant les branches de l'arbre. Les hachages intérieurs n'ont pas besoin d'être stockés.

Un en-tête de bloc sans transactions ferait environ 80 octets. Si nous supposons que les blocs sont générés toutes les 10 minutes, 80 octets 6 24 * 365 = 4,2 Mo par an. Avec des systèmes informatiques vendus généralement avec 2 Go de RAM à partir de 2008 et la loi de Moore prévoyant une croissance actuelle de 1,2 Go par an, le stockage ne devrait pas poser de problème même si les en-têtes de bloc doivent être conservés en mémoire.
8. Vérification simplifiée des paiements
Il est possible de vérifier les paiements sans exécuter un nœud de réseau complet. Un utilisateur doit uniquement conserver une copie des en-têtes de bloc de la chaîne de preuve de travail la plus longue, qu'il peut obtenir en interrogeant les nœuds du réseau jusqu'à ce qu'il soit convaincu qu'il possède la chaîne la plus longue, et obtenir la branche Merkle reliant la transaction au bloc. son horodatage. Il ne peut pas vérifier la transaction par lui-même, mais en la reliant à un endroit de la chaîne, il peut voir qu'un nœud du réseau l'a acceptée et les blocs ajoutés après confirment que le réseau l'a acceptée.

En tant que telle, la vérification est fiable tant que des nœuds honnêtes contrôlent le réseau, mais elle est plus vulnérable si le réseau est maîtrisé par un attaquant. Même si les nœuds du réseau peuvent vérifier les transactions par eux-mêmes, la méthode simplifiée peut être trompée par les transactions fabriquées par un attaquant aussi longtemps que celui-ci peut continuer à maîtriser le réseau. Une stratégie pour se protéger contre cela serait d'accepter les alertes des nœuds du réseau lorsqu'ils détectent un bloc invalide, invitant le logiciel de l'utilisateur à télécharger le bloc complet et à alerter les transactions pour confirmer l'incohérence. Les entreprises qui reçoivent des paiements fréquents voudront probablement toujours exécuter leurs propres nœuds pour une sécurité plus indépendante et une vérification plus rapide.
9. Combinaison et fractionnement de la valeur
Bien qu’il soit possible de gérer les pièces individuellement, il serait difficile d’effectuer une transaction distincte pour chaque centime d’un transfert. Pour permettre de diviser et de combiner la valeur, les transactions contiennent plusieurs entrées et sorties. Normalement, il y aura soit une seule entrée provenant d'une transaction précédente plus importante, soit plusieurs entrées combinant des montants plus petits, et au plus deux sorties : une pour le paiement et une pour renvoyer la monnaie, le cas échéant, à l'expéditeur.

Il convient de noter que la répartition, dans laquelle une transaction dépend de plusieurs transactions, et ces transactions dépendent de beaucoup plus, ne pose pas ici de problème. Il n'est jamais nécessaire d'extraire une copie autonome complète de l'historique d'une transaction.
10. Confidentialité
Le modèle bancaire traditionnel atteint un certain niveau de confidentialité en limitant l'accès aux informations aux parties impliquées et au tiers de confiance. La nécessité d'annoncer publiquement toutes les transactions exclut cette méthode, mais la confidentialité peut toujours être préservée en interrompant le flux d'informations vers un autre endroit : en gardant les clés publiques anonymes. Le public peut voir que quelqu’un envoie un montant à quelqu’un d’autre, mais sans information liant la transaction à qui que ce soit. Ceci est similaire au niveau d'information publié par les bourses, où l'heure et la taille des transactions individuelles, la « bande », sont rendues publiques, mais sans révéler qui étaient les parties.

En tant que pare-feu supplémentaire, une nouvelle paire de clés doit être utilisée pour chaque transaction afin d'éviter qu'elles ne soient liées à un propriétaire commun. Certains liens restent inévitables dans les transactions à intrants multiples, qui révèlent nécessairement que leurs intrants appartenaient au même propriétaire. Le risque est que si le propriétaire d’une clé est révélé, la liaison pourrait révéler d’autres transactions appartenant au même propriétaire.
11. Calculs
Nous considérons le scénario d’un attaquant essayant de générer une chaîne alternative plus rapidement que la chaîne honnête. Même si cela est accompli, cela n’expose pas le système à des changements arbitraires, comme créer de la valeur à partir de rien ou prendre de l’argent qui n’a jamais appartenu à l’attaquant. Les nœuds n'accepteront pas une transaction invalide comme paiement, et les nœuds honnêtes n'accepteront jamais un bloc les contenant. Un attaquant ne peut tenter de modifier qu’une de ses propres transactions pour récupérer l’argent qu’il a récemment dépensé. La course entre la chaîne honnête et une chaîne attaquante peut être caractérisée comme une marche aléatoire binomiale. L'événement de réussite est l'extension de la chaîne honnête d'un bloc, augmentant son avance de +1, et l'événement d'échec est l'extension de la chaîne de l'attaquant d'un bloc, réduisant l'écart de -1.
La probabilité qu'un attaquant rattrape un déficit donné est analogue au problème de la ruine du joueur. Supposons qu'un joueur disposant d'un crédit illimité commence avec un déficit et joue potentiellement un nombre infini d'essais pour tenter d'atteindre le seuil de rentabilité. Nous pouvons calculer la probabilité qu’il atteigne le seuil de rentabilité, ou qu’un attaquant rattrape un jour la chaîne honnête, comme suit [8] :
p = probabilité qu'un nœud honnête trouve le bloc suivant
q = probabilité que l'attaquant trouve le bloc suivant
qz = probabilité que l'attaquant rattrape un jour z blocs derrière
qz= { 1 si p≤q
(q/ p)^z si p>q}
Étant donné notre hypothèse selon laquelle p > q, la probabilité diminue de façon exponentielle à mesure que le nombre de blocs que l'attaquant doit rattraper augmente. Avec les chances contre lui, s'il ne fait pas un saut chanceux dès le début, ses chances deviennent infimes à mesure qu'il prend du retard.
Nous examinons maintenant combien de temps le destinataire d'une nouvelle transaction doit attendre avant d'être suffisamment certain que l'expéditeur ne peut pas modifier la transaction. Nous supposons que l'expéditeur est un attaquant qui veut faire croire au destinataire qu'il l'a payé pendant un certain temps, puis le faire se rembourser après un certain temps. Le destinataire sera alerté lorsque cela se produira, mais l’expéditeur espère qu’il sera trop tard.
Le destinataire génère une nouvelle paire de clés et donne la clé publique à l'expéditeur peu de temps avant de signer. Cela empêche l'expéditeur de préparer une chaîne de blocs à l'avance en travaillant dessus en continu jusqu'à ce qu'il ait la chance d'avancer suffisamment loin, puis d'exécuter la transaction à ce moment-là. Une fois la transaction envoyée, l’expéditeur malhonnête commence à travailler en secret sur une chaîne parallèle contenant une version alternative de sa transaction.
Le destinataire attend que la transaction ait été ajoutée à un bloc et que z blocs aient été liés après celle-ci. Il ne connaît pas la progression exacte de l'attaquant, mais en supposant que les blocages honnêtes ont pris le temps moyen attendu par bloc, la progression potentielle de l'attaquant sera une distribution de Poisson avec une valeur attendue :

Conversion en code C...

En exécutant certains résultats, nous pouvons voir la probabilité diminuer de façon exponentielle avec z.
q=0,1
z=0 P=1.0000000
z = 1 P = 0,2045873
z = 2 P = 0,0509779
z = 3 P = 0,0131722
z=4 P=0,0034552
z = 5 P = 0,0009137
z=6P=0,0002428
z = 7 P = 0,0000647
z=8P=0,0000173
z=9P=0,0000046
z=10P=0,0000012
q=0,3
z=0 P=1.0000000
z = 5 P = 0,1773523
z=10P=0,0416605
z=15P=0,0101008
z=20P=0,0024804
z=25P=0,0006132
z=30P=0,0001522
z=35P=0,0000379
z=40P=0,0000095
z=45P=0,0000024
z=50P=0,0000006
Résolution de P inférieur à 0,1%...
P < 0,001
q=0,10z=5
q=0,15z=8
q=0,20 z=11
q=0,25z=15
q=0,30z=24
q=0,35z=41
q=0,40z=89
q=0,45z=340
12. Conclusion
Nous avons proposé un système de transactions électroniques sans confiance. Nous avons commencé avec le cadre habituel de pièces fabriquées à partir de signatures numériques, qui offre un contrôle fort de la propriété, mais est incomplet sans un moyen d'empêcher les doubles dépenses. Pour résoudre ce problème, nous avons proposé un réseau peer-to-peer utilisant une preuve de travail pour enregistrer un historique public des transactions qui devient rapidement impossible à modifier pour un attaquant si des nœuds honnêtes contrôlent la majorité de la puissance du processeur. Le réseau est robuste dans sa simplicité non structurée. Les nœuds fonctionnent en même temps avec peu de coordination. Il n'est pas nécessaire de les identifier, car les messages ne sont acheminés vers aucun endroit particulier et doivent uniquement être transmis dans la mesure du possible. Les nœuds peuvent quitter et rejoindre le réseau à volonté, acceptant la chaîne de preuve de travail comme preuve de ce qui s'est passé pendant leur absence. Ils votent avec la puissance de leur CPU, exprimant leur acceptation des blocs valides en travaillant à leur extension et en rejetant les blocs invalides en refusant de travailler dessus. Toutes les règles et incitations nécessaires peuvent être appliquées grâce à ce mécanisme de consensus.
Les références
[1] W. Dai, « b-money », http://www.weidai.com/bmoney.txt, 1998.
[2] H. Massias, X.S. Avila et J.-J. Quisquater, "Conception d'un service d'horodatage sécurisé avec un minimum
exigences de confiance », lors du 20e Symposium sur la théorie de l'information au Benelux, mai 1999.
[3] S. Haber, WS et al. Stornetta, "Comment horodater un document numérique", dans Journal of Cryptology, vol 3, non
2, pages 99-111, 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, "Améliorer l'efficacité et la fiabilité de l'horodatage numérique",
Dans Séquences II : Méthodes en communication, sécurité et informatique, pages 329-334, 1993.
[5] S. Haber, WS et al. Stornetta, « Noms sécurisés pour les chaînes de bits », dans les actes de la 4e conférence ACM
sur la sécurité informatique et des communications, pages 28-35, avril 1997.
[6] A. Back, "Hashcash - une contre-mesure en cas de déni de service",
http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] R.C. Merkle, « Protocoles pour les cryptosystèmes à clé publique », dans Proc. Symposium de 1980 sur la sécurité et
Confidentialité, IEEE Computer Society, pages 122-133, avril 1980.
[8] W. Feller, « Une introduction à la théorie des probabilités et ses applications », 1957.



