Satoshi Nakamoto
satoshin@gmx.com
www.bitcoin.org

Zusammenfassung: Eine reine Peer-to-Peer-Version von elektronischem Bargeld würde es ermöglichen, Online-Zahlungen direkt von einer Partei zur anderen zu senden, ohne den Umweg über ein Finanzinstitut. Digitale Signaturen stellen einen Teil der Lösung dar, aber die Hauptvorteile gehen verloren, wenn weiterhin ein vertrauenswürdiger Dritter erforderlich ist, um Doppelausgaben zu verhindern. Wir schlagen eine Lösung für das Problem der doppelten Ausgaben mithilfe eines Peer-to-Peer-Netzwerks vor. Das Netzwerk versieht Transaktionen mit einem Zeitstempel, indem es sie in eine fortlaufende Kette von Hash-basierten Arbeitsnachweisen einfügt und so einen Datensatz erstellt, der nicht geändert werden kann, ohne den Arbeitsnachweis zu wiederholen. Die längste Kette dient nicht nur als Beweis für die Abfolge der beobachteten Ereignisse, sondern auch als Beweis dafür, dass sie aus dem größten Pool an CPU-Leistung stammt. Solange ein Großteil der CPU-Leistung von Knoten kontrolliert wird, die nicht kooperieren, um das Netzwerk anzugreifen, erzeugen sie die längste Kette und übertreffen die Angreifer. Das Netzwerk selbst erfordert eine minimale Struktur. Nachrichten werden nach dem Best-Effort-Prinzip gesendet und Knoten können das Netzwerk nach Belieben verlassen und wieder beitreten, wobei sie die längste Proof-of-Work-Kette als Beweis dafür akzeptieren, was während ihrer Abwesenheit passiert ist.
1. Einleitung
Der Handel im Internet verlässt sich mittlerweile fast ausschließlich auf Finanzinstitute, die als vertrauenswürdige Drittparteien fungieren, um elektronische Zahlungen abzuwickeln. Obwohl das System für die meisten Transaktionen gut genug funktioniert, leidet es immer noch unter den inhärenten Schwächen des auf Vertrauen basierenden Modells. Vollständig nicht umkehrbare Transaktionen sind nicht wirklich möglich, da Finanzinstitute nicht umhin kommen, bei Streitigkeiten zu vermitteln. Die Kosten der Vermittlung erhöhen die Transaktionskosten, begrenzen die minimale praktische Transaktionsgröße und schließen die Möglichkeit kleiner, gelegentlicher Transaktionen aus. Darüber hinaus entstehen noch höhere Kosten durch den Verlust der Möglichkeit, nicht umkehrbare Zahlungen für nicht umkehrbare Dienste zu leisten. Mit der Möglichkeit der Rückabwicklung steigt auch die Notwendigkeit des Vertrauens. Händler müssen gegenüber ihren Kunden vorsichtig sein und sie nach mehr Informationen fragen, als sie sonst benötigen würden. Ein gewisser Prozentsatz an Betrug wird als unvermeidlich akzeptiert. Diese Kosten und Zahlungsunsicherheiten können persönlich durch die Verwendung physischer Währung vermieden werden, es gibt jedoch keinen Mechanismus, um Zahlungen über einen Kommunikationskanal ohne eine vertrauenswürdige Partei zu tätigen.
Was wir brauchen, ist ein elektronisches Zahlungssystem, das auf kryptografischen Beweisen statt auf Vertrauen basiert und es zwei beliebigen Parteien ermöglicht, direkt miteinander Geschäfte zu tätigen, ohne dass eine vertrauenswürdige dritte Partei erforderlich ist. Transaktionen, deren Rückgängigmachung rechnerisch unmöglich ist, würden Verkäufer vor Betrug schützen, und zum Schutz der Käufer könnten problemlos routinemäßige Treuhandmechanismen implementiert werden. In diesem Artikel schlagen wir eine Lösung für das Problem der Doppelausgaben vor, bei der ein Peer-to-Peer-Zeitstempelserver verwendet wird, um einen rechnerischen Beweis für die chronologische Reihenfolge der Transaktionen zu generieren. Das System ist sicher, solange ehrliche Knoten gemeinsam mehr CPU-Leistung kontrollieren als jede kooperierende Gruppe von Angreiferknoten.
2. Transaktionen
Wir definieren eine elektronische Münze als eine Kette digitaler Signaturen. Jeder Besitzer überträgt die Münze an den nächsten, indem er einen Hash der vorherigen Transaktion und den öffentlichen Schlüssel des nächsten Besitzers digital signiert und diese am Ende der Münze anfügt. Ein Zahlungsempfänger kann die Signaturen überprüfen, um die Eigentumskette zu verifizieren.

Das Problem besteht natürlich darin, dass der Zahlungsempfänger nicht überprüfen kann, ob einer der Besitzer die Münze nicht doppelt ausgegeben hat. Eine gängige Lösung besteht darin, eine vertrauenswürdige zentrale Behörde oder Münzprägeanstalt einzuführen, die jede Transaktion auf Doppelausgabe überprüft. Nach jeder Transaktion muss die Münze an die Münzprägeanstalt zurückgegeben werden, damit eine neue Münze ausgegeben werden kann. Nur bei Münzen, die direkt von der Münzprägeanstalt ausgegeben werden, kann man sich darauf verlassen, dass sie nicht doppelt ausgegeben werden. Das Problem bei dieser Lösung besteht darin, dass das Schicksal des gesamten Geldsystems von dem Unternehmen abhängt, das die Münzprägeanstalt betreibt, und jede Transaktion muss durch sie laufen, genau wie bei einer Bank. Wir brauchen eine Möglichkeit, damit der Zahlungsempfänger weiß, dass die vorherigen Besitzer keine früheren Transaktionen unterzeichnet haben. Für unsere Zwecke zählt die früheste Transaktion, daher kümmern wir uns nicht um spätere Versuche der Doppelausgabe. Die einzige Möglichkeit, das Fehlen einer Transaktion zu bestätigen, besteht darin, über alle Transaktionen informiert zu sein. Im auf der Münzprägeanstalt basierenden Modell war die Münzprägeanstalt über alle Transaktionen informiert und entschied, welche zuerst eintraf. Um dies ohne eine vertrauenswürdige Partei zu erreichen, müssen Transaktionen öffentlich bekannt gegeben werden [1], und wir brauchen ein System, bei dem sich die Teilnehmer auf eine einheitliche Historie der Reihenfolge einigen können, in der sie empfangen wurden. Der Zahlungsempfänger braucht den Nachweis, dass zum Zeitpunkt jeder Transaktion die Mehrheit der Knoten darin übereinstimmte, dass die Transaktion als erste empfangen wurde.
3. Zeitstempelserver
Die von uns vorgeschlagene Lösung beginnt mit einem Zeitstempelserver. Ein Zeitstempelserver funktioniert, indem er einen Hash eines Blocks von Elementen erstellt, die mit einem Zeitstempel versehen werden sollen, und diesen Hash weithin veröffentlicht, beispielsweise in einer Zeitung oder einem Usenet-Post [2-5]. Der Zeitstempel beweist, dass die Daten zu diesem Zeitpunkt existiert haben müssen, um in den Hash zu gelangen. Jeder Zeitstempel enthält den vorherigen Zeitstempel in seinem Hash und bildet so eine Kette, wobei jeder zusätzliche Zeitstempel die vorherigen verstärkt.

4. Arbeitsnachweis
Um einen verteilten Zeitstempelserver auf Peer-to-Peer-Basis zu implementieren, müssen wir ein Proof-of-Work-System ähnlich Adam Backs Hashcash [6] verwenden, statt Zeitungs- oder Usenet-Posts. Der Proof-of-Work beinhaltet das Suchen nach einem Wert, der beim Hashen, beispielsweise mit SHA-256, mit einer Anzahl von Nullbits beginnt. Der durchschnittlich erforderliche Arbeitsaufwand ist exponentiell zur Anzahl der erforderlichen Nullbits und kann durch Ausführen eines einzelnen Hashs überprüft werden.
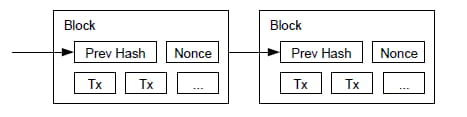
Für unser Zeitstempelnetzwerk implementieren wir den Proof-of-Work, indem wir einen Nonce im Block erhöhen, bis ein Wert gefunden wird, der dem Hash des Blocks die erforderlichen Nullbits gibt. Sobald der CPU-Aufwand aufgewendet wurde, um den Proof-of-Work zu erfüllen, kann der Block nicht mehr geändert werden, ohne die Arbeit zu wiederholen. Da spätere Blöcke danach verkettet werden, würde die Arbeit zum Ändern des Blocks das Wiederholen aller Blöcke danach beinhalten.
Der Proof-of-Work löst auch das Problem der Bestimmung der Repräsentation bei Mehrheitsentscheidungen. Wenn die Mehrheit auf „eine IP-Adresse, eine Stimme“ basieren würde, könnte sie von jedem unterwandert werden, der viele IPs zuteilen kann. Proof-of-Work ist im Wesentlichen „eine CPU, eine Stimme“. Die Mehrheitsentscheidung wird durch die längste Kette repräsentiert, in die der größte Proof-of-Work-Aufwand investiert wurde. Wenn die Mehrheit der CPU-Leistung von ehrlichen Knoten kontrolliert wird, wird die ehrliche Kette am schnellsten wachsen und alle konkurrierenden Ketten überholen. Um einen früheren Block zu ändern, müsste ein Angreifer den Proof-of-Work des Blocks und aller Blöcke danach wiederholen und dann die Arbeit der ehrlichen Knoten einholen und übertreffen. Wir werden später zeigen, dass die Wahrscheinlichkeit, dass ein langsamerer Angreifer aufholt, exponentiell abnimmt, wenn weitere Blöcke hinzugefügt werden.
Um die zunehmende Hardwaregeschwindigkeit und das im Laufe der Zeit variierende Interesse an laufenden Knoten auszugleichen, wird die Proof-of-Work-Schwierigkeit durch einen gleitenden Durchschnitt bestimmt, der auf eine durchschnittliche Anzahl von Blöcken pro Stunde abzielt. Wenn sie zu schnell generiert werden, steigt die Schwierigkeit.
5. Netzwerk
Die Schritte zum Ausführen des Netzwerks sind wie folgt:
1) Neue Transaktionen werden an alle Knoten gesendet.
2) Jeder Knoten sammelt neue Transaktionen in einem Block.
3) Jeder Knoten arbeitet daran, einen schwierigen Arbeitsnachweis für seinen Block zu finden.
4) Wenn ein Knoten einen Arbeitsnachweis findet, sendet er den Block an alle Knoten.
5) Knoten akzeptieren den Block nur, wenn alle darin enthaltenen Transaktionen gültig und noch nicht ausgegeben sind.
6) Knoten drücken ihre Akzeptanz des Blocks aus, indem sie an der Erstellung des nächsten Blocks in der Kette arbeiten und dabei den Hash des akzeptierten Blocks als vorherigen Hash verwenden.
Knoten betrachten die längste Kette immer als die richtige und arbeiten weiter an ihrer Erweiterung. Wenn zwei Knoten gleichzeitig unterschiedliche Versionen des nächsten Blocks senden, erhalten einige Knoten möglicherweise zuerst die eine oder die andere. In diesem Fall arbeiten sie an der zuerst empfangenen Version, speichern aber den anderen Zweig für den Fall, dass dieser länger wird. Der Gleichstand wird aufgelöst, wenn der nächste Arbeitsnachweis gefunden wird und ein Zweig länger wird; die Knoten, die an dem anderen Zweig gearbeitet haben, wechseln dann zu dem längeren.
Neue Transaktionsübertragungen müssen nicht unbedingt alle Knoten erreichen. Solange sie viele Knoten erreichen, werden sie innerhalb kurzer Zeit in einen Block gelangen. Blockübertragungen sind auch tolerant gegenüber verlorenen Nachrichten. Wenn ein Knoten einen Block nicht empfängt, wird er ihn anfordern, wenn er den nächsten Block empfängt und feststellt, dass er einen verpasst hat.
6. Anreiz
Konventionell ist die erste Transaktion in einem Block eine spezielle Transaktion, die eine neue Münze startet, die dem Ersteller des Blocks gehört. Dies bietet den Knoten einen Anreiz, das Netzwerk zu unterstützen, und bietet eine Möglichkeit, Münzen zunächst in Umlauf zu bringen, da es keine zentrale Behörde gibt, die sie ausgibt. Das stetige Hinzufügen einer konstanten Menge neuer Münzen ist analog zu Goldgräbern, die Ressourcen aufwenden, um Gold in Umlauf zu bringen. In unserem Fall werden CPU-Zeit und Strom verbraucht.
Der Anreiz kann auch durch Transaktionsgebühren finanziert werden. Wenn der Ausgabewert einer Transaktion geringer ist als ihr Eingabewert, ist die Differenz eine Transaktionsgebühr, die zum Anreizwert des Blocks hinzugefügt wird, der die Transaktion enthält. Sobald eine vorher festgelegte Anzahl von Münzen in Umlauf gekommen ist, kann der Anreiz vollständig auf Transaktionsgebühren umgestellt werden und ist völlig inflationsfrei.
Der Anreiz könnte dazu beitragen, dass die Knoten ehrlich bleiben. Wenn ein gieriger Angreifer mehr CPU-Leistung anhäufen kann als alle ehrlichen Knoten, muss er sich entscheiden, ob er diese Leistung nutzt, um Leute zu betrügen, indem er ihnen ihre Zahlungen stiehlt, oder ob er sie nutzt, um neue Münzen zu generieren. Er sollte es profitabler finden, sich an die Regeln zu halten, die ihm mehr neue Münzen bescheren als allen anderen zusammen, als das System und die Gültigkeit seines eigenen Reichtums zu untergraben.
7. Speicherplatz freigeben
Sobald die letzte Transaktion einer Münze unter genügend Blöcken vergraben ist, können die davor ausgegebenen Transaktionen verworfen werden, um Speicherplatz zu sparen. Um dies zu ermöglichen, ohne den Hash des Blocks zu beschädigen, werden Transaktionen in einem Merkle-Baum [7][2][5] gehasht, wobei nur die Wurzel im Hash des Blocks enthalten ist. Alte Blöcke können dann komprimiert werden, indem Zweige des Baums abgetrennt werden. Die inneren Hashes müssen nicht gespeichert werden.

Ein Blockheader ohne Transaktionen wäre etwa 80 Bytes groß. Wenn wir davon ausgehen, dass alle 10 Minuten Blöcke generiert werden, sind das 80 Bytes 6 24 * 365 = 4,2 MB pro Jahr. Da Computersysteme seit 2008 typischerweise mit 2 GB RAM verkauft werden und Moores Gesetz ein aktuelles Wachstum von 1,2 GB pro Jahr vorhersagt, sollte die Speicherung kein Problem darstellen, selbst wenn die Blockheader im Speicher gehalten werden müssen.
8. Vereinfachte Zahlungsüberprüfung
Es ist möglich, Zahlungen zu verifizieren, ohne einen vollständigen Netzwerkknoten auszuführen. Ein Benutzer muss lediglich eine Kopie der Blockheader der längsten Proof-of-Work-Kette aufbewahren, die er erhalten kann, indem er Netzwerkknoten abfragt, bis er überzeugt ist, dass er die längste Kette hat, und den Merkle-Zweig erhält, der die Transaktion mit dem Block verknüpft, in dem sie mit einem Zeitstempel versehen ist. Er kann die Transaktion nicht selbst überprüfen, aber indem er sie mit einer Stelle in der Kette verknüpft, kann er sehen, dass ein Netzwerkknoten sie akzeptiert hat, und Blöcke, die danach hinzugefügt werden, bestätigen zusätzlich, dass das Netzwerk sie akzeptiert hat.

Die Verifizierung ist also zuverlässig, solange ehrliche Knoten das Netzwerk kontrollieren, ist aber anfälliger, wenn das Netzwerk von einem Angreifer überwältigt wird. Während Netzwerkknoten Transaktionen selbst verifizieren können, kann die vereinfachte Methode durch die erfundenen Transaktionen eines Angreifers getäuscht werden, solange dieser das Netzwerk weiterhin überwältigen kann. Eine Strategie zum Schutz davor wäre, Warnungen von Netzwerkknoten zu akzeptieren, wenn diese einen ungültigen Block erkennen. Dadurch wird die Software des Benutzers aufgefordert, den vollständigen Block herunterzuladen und Transaktionen zu melden, um die Inkonsistenz zu bestätigen. Unternehmen, die häufig Zahlungen erhalten, werden wahrscheinlich trotzdem ihre eigenen Knoten betreiben wollen, um eine unabhängigere Sicherheit und eine schnellere Verifizierung zu gewährleisten.
9. Kombinieren und Aufteilen von Werten
Obwohl es möglich wäre, Münzen einzeln zu handhaben, wäre es unhandlich, für jeden Cent einer Überweisung eine separate Transaktion durchzuführen. Um das Aufteilen und Kombinieren von Werten zu ermöglichen, enthalten Transaktionen mehrere Ein- und Ausgaben. Normalerweise gibt es entweder eine einzelne Eingabe aus einer größeren vorherigen Transaktion oder mehrere Eingaben, die kleinere Beträge kombinieren, und höchstens zwei Ausgaben: eine für die Zahlung und eine, die das Wechselgeld, falls vorhanden, an den Absender zurückgibt.

Es ist zu beachten, dass Fan-Out, bei dem eine Transaktion von mehreren Transaktionen abhängt und diese Transaktionen wiederum von vielen weiteren, hier kein Problem darstellt. Es besteht nie die Notwendigkeit, eine vollständige, eigenständige Kopie des Verlaufs einer Transaktion zu extrahieren.
10. Datenschutz
Das traditionelle Bankmodell erreicht ein gewisses Maß an Privatsphäre, indem es den Zugang zu Informationen auf die beteiligten Parteien und die vertrauenswürdige dritte Partei beschränkt. Die Notwendigkeit, alle Transaktionen öffentlich bekannt zu geben, schließt diese Methode aus, aber die Privatsphäre kann trotzdem gewahrt werden, indem der Informationsfluss an einer anderen Stelle unterbrochen wird: indem öffentliche Schlüssel anonym gehalten werden. Die Öffentlichkeit kann sehen, dass jemand einen Betrag an jemand anderen sendet, aber ohne Informationen, die die Transaktion mit irgendjemandem in Verbindung bringen. Dies ist vergleichbar mit dem Informationsniveau, das von Börsen freigegeben wird, wo der Zeitpunkt und die Größe einzelner Transaktionen, das „Tape“, öffentlich gemacht werden, aber ohne zu sagen, wer die Beteiligten waren.

Als zusätzliche Firewall sollte für jede Transaktion ein neues Schlüsselpaar verwendet werden, um zu verhindern, dass sie einem gemeinsamen Besitzer zugeordnet werden. Bei Transaktionen mit mehreren Eingaben, die zwangsläufig offenbaren, dass ihre Eingaben demselben Besitzer gehörten, ist eine gewisse Verknüpfung immer noch unvermeidlich. Das Risiko besteht darin, dass, wenn der Besitzer eines Schlüssels offengelegt wird, durch die Verknüpfung andere Transaktionen offengelegt werden könnten, die demselben Besitzer gehörten.
11. Berechnungen
Wir betrachten das Szenario eines Angreifers, der versucht, eine alternative Kette schneller als die ehrliche Kette zu generieren. Selbst wenn dies gelingt, ist das System dadurch nicht für willkürliche Änderungen anfällig, wie etwa die Schaffung von Wert aus dem Nichts oder die Entnahme von Geld, das dem Angreifer nie gehört hat. Knoten werden keine ungültigen Transaktionen als Zahlung akzeptieren, und ehrliche Knoten werden niemals einen Block akzeptieren, der sie enthält. Ein Angreifer kann nur versuchen, eine seiner eigenen Transaktionen zu ändern, um Geld zurückzubekommen, das er kürzlich ausgegeben hat. Das Rennen zwischen der ehrlichen Kette und einer Angreiferkette kann als binomialer Zufallsgang charakterisiert werden. Das Erfolgsereignis ist die Verlängerung der ehrlichen Kette um einen Block, wodurch sich ihr Vorsprung um +1 vergrößert, und das Misserfolgsereignis ist die Verlängerung der Kette des Angreifers um einen Block, wodurch sich der Abstand um -1 verringert.
Die Wahrscheinlichkeit, dass ein Angreifer ein bestimmtes Defizit wieder aufholt, ist analog zum Problem des Ruins eines Spielers. Angenommen, ein Spieler mit unbegrenztem Kredit startet mit einem Defizit und spielt potenziell unendlich viele Versuche, um die Gewinnschwelle zu erreichen. Wir können die Wahrscheinlichkeit, dass er jemals die Gewinnschwelle erreicht, oder dass ein Angreifer jemals die ehrliche Kette einholt, wie folgt berechnen [8]:
p = Wahrscheinlichkeit, dass ein ehrlicher Knoten den nächsten Block findet
q = Wahrscheinlichkeit, dass der Angreifer den nächsten Block findet
qz = Wahrscheinlichkeit, dass der Angreifer ihn jemals aus einer Entfernung von z Blöcken einholt
qz= { 1 wenn p≤q
(q/ p)^z wenn p>q}
Unter der Annahme, dass p > q, sinkt die Wahrscheinlichkeit exponentiell, wenn die Anzahl der Blöcke zunimmt, die der Angreifer aufholen muss. Wenn ihm die Chancen gegen den Angreifer stehen und er nicht früh einen glücklichen Vorstoß nach vorne schafft, werden seine Chancen verschwindend gering, je weiter er zurückfällt.
Wir überlegen nun, wie lange der Empfänger einer neuen Transaktion warten muss, bis er ausreichend sicher ist, dass der Absender die Transaktion nicht ändern kann. Wir gehen davon aus, dass der Absender ein Angreifer ist, der dem Empfänger eine Zeit lang vorgaukeln will, er habe ihm das Geld bezahlt, und es dann nach einiger Zeit so umstellen will, dass er sich selbst das Geld zurückzahlt. Der Empfänger wird benachrichtigt, wenn das passiert, aber der Absender hofft, dass es zu spät ist.
Der Empfänger generiert ein neues Schlüsselpaar und gibt den öffentlichen Schlüssel kurz vor der Unterzeichnung an den Absender weiter. Dies verhindert, dass der Absender im Voraus eine Kette von Blöcken vorbereitet, indem er kontinuierlich daran arbeitet, bis er das Glück hat, weit genug voranzukommen, und dann in diesem Moment die Transaktion ausführt. Sobald die Transaktion gesendet ist, beginnt der unehrliche Absender im Geheimen an einer parallelen Kette zu arbeiten, die eine alternative Version seiner Transaktion enthält.
Der Empfänger wartet, bis die Transaktion zu einem Block hinzugefügt wurde und danach z Blöcke verknüpft wurden. Er kennt den genauen Fortschritt des Angreifers nicht, aber unter der Annahme, dass die ehrlichen Blöcke die durchschnittlich erwartete Zeit pro Block benötigten, wird der potenzielle Fortschritt des Angreifers eine Poisson-Verteilung mit dem erwarteten Wert sein:

Konvertieren in C-Code ...

Wenn wir einige Ergebnisse ausführen, können wir sehen, dass die Wahrscheinlichkeit exponentiell mit z abfällt.
q = 0,1
z=0 P=1,0000000
z=1 P=0,2045873
z=2 P=0,0509779
z=3 P=0,0131722
z=4 P=0,0034552
z=5 P=0,0009137
z=6 P=0,0002428
z=7 P=0,0000647
z=8 P=0,0000173
z=9 P=0,0000046
z=10 P=0,0000012
q = 0,3
z=0 P=1,0000000
z=5 P=0,1773523
z=10 P=0,0416605
z=15 P=0,0101008
z=20 P=0,0024804
z=25 P=0,0006132
z=30 P=0,0001522
z=35 P=0,0000379
z=40 P=0,0000095
z=45 P=0,0000024
z=50 P=0,0000006
Lösung für P kleiner als 0,1 % …
P < 0,001
q=0,10 z=5
q=0,15 z=8
q=0,20 z=11
q=0,25 z=15
q=0,30 z=24
q=0,35 z=41
q=0,40 z=89
q=0,45 z=340
12. Fazit
Wir haben ein System für elektronische Transaktionen vorgeschlagen, das nicht auf Vertrauen beruht. Wir begannen mit dem üblichen Rahmenwerk von Münzen aus digitalen Signaturen, das eine starke Kontrolle des Eigentums bietet, aber ohne eine Möglichkeit zur Verhinderung von Doppelausgaben unvollständig ist. Um dieses Problem zu lösen, schlugen wir ein Peer-to-Peer-Netzwerk vor, das Proof-of-Work verwendet, um einen öffentlichen Transaktionsverlauf aufzuzeichnen, der für einen Angreifer schnell rechnerisch unpraktisch wird, wenn ehrliche Knoten die Mehrheit der CPU-Leistung kontrollieren. Das Netzwerk ist in seiner unstrukturierten Einfachheit robust. Knoten arbeiten alle gleichzeitig und mit wenig Koordination. Sie müssen nicht identifiziert werden, da Nachrichten nicht an einen bestimmten Ort weitergeleitet werden und nur nach bestem Wissen und Gewissen zugestellt werden müssen. Knoten können das Netzwerk nach Belieben verlassen und wieder betreten und akzeptieren die Proof-of-Work-Kette als Beweis dafür, was während ihrer Abwesenheit passiert ist. Sie stimmen mit ihrer CPU-Leistung ab und drücken ihre Akzeptanz gültiger Blöcke aus, indem sie an deren Erweiterung arbeiten, und lehnen ungültige Blöcke ab, indem sie sich weigern, an ihnen zu arbeiten. Alle erforderlichen Regeln und Anreize können mit diesem Konsensmechanismus durchgesetzt werden.
Verweise
[1] W. Dai, „b-money“, http://www.weidai.com/bmoney.txt, 1998.
[2] H. Massias, X.S. Avila und J.-J. Quisquater, „Entwurf eines sicheren Zeitstempeldienstes mit minimaler
Vertrauensanforderungen“, im 20. Symposium zur Informationstheorie in den Benelux-Ländern, Mai 1999.
[3] S. Haber, W.S. Stornetta, "Wie man ein digitales Dokument mit einem Zeitstempel versieht", In Journal of Cryptology, Band 3, Nr.
2, Seiten 99-111, 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, „Verbesserung der Effizienz und Zuverlässigkeit digitaler Zeitstempel“,
In Sequences II: Methoden in Kommunikation, Sicherheit und Informatik, Seiten 329-334, 1993.
[5] S. Haber, W.S. Stornetta, „Sichere Namen für Bitstrings“, In Proceedings der 4. ACM-Konferenz
zur Computer- und Kommunikationssicherheit, Seiten 28-35, April 1997.
[6] A. Back, „Hashcash - eine Denial-of-Service-Gegenmaßnahme“,
http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] R.C. Merkle, „Protokolle für Public-Key-Kryptosysteme“, In Proc. 1980 Symposium über Sicherheit und
Datenschutz, IEEE Computer Society, Seiten 122–133, April 1980.
[8] W. Feller, „Eine Einführung in die Wahrscheinlichkeitstheorie und ihre Anwendungen“, 1957.



